Murmurhash初步学习

阅读英文版本

Murmurhash是由Austin Appleby在2008年发明的一种非常简单的、不具有加密特性的散列函数，可以非常容易地应用在常见的基于散列的查找场景中。Murmurhash非常简单，在X86体系结构的机器上可以用少于52条指令完成所有的计算，由此带来的性能也是非常优秀的。此外，Murmurhash具有非常好的强混淆性（雪崩效应）和非常低的冲突风险。强混淆性指的是输入数据的微小改变，都会产生一个完全不同的散列值，这使得借助Murmurhash计算得到的散列值具有非常优秀的分布性。Murmurhash的当前版本是Murmurhash3，可以用来生成一个32位或128的散列值。如果生成结果是128位结果，那么在X86结构和X64结构上的计算结果是不一样的。本文以Murmurhash2为例进行讨论。

作者在C版本的代码中对Murmurhash的运行提出了一些假设和解释：

假设系统可以一次性读取4个字节；
假设int类型数据的长度是4个字节；
算法不会按照增量的方式工作；
算法在大端（big-endian）和小端（little-endian）结构下的执行结果不一致。

下面我将以32位版本为例进行学习（下述代码由Jedis 3.2.0实现）：

public static int hash(ByteBuffer buf, int seed) {
    // save byte order for later restoration
    ByteOrder byteOrder = buf.order();
    buf.order(ByteOrder.LITTLE_ENDIAN);

    int m = 0x5bd1e995;
    int r = 24;

    int h = seed ^ buf.remaining();

    int k;
    while (buf.remaining() >= 4) {
      k = buf.getInt();

      k *= m;
      k ^= k >>> r;
      k *= m;

      h *= m;
      h ^= k;
    }

    if (buf.remaining() > 0) {
      ByteBuffer finish = ByteBuffer.allocate(4).order(ByteOrder.LITTLE_ENDIAN);
      // for big-endian version, use this first:
      // finish.position(4-buf.remaining());
      finish.put(buf).rewind();
      h ^= finish.getInt();
      h *= m;
    }

    h ^= h >>> 13;
    h *= m;
    h ^= h >>> 15;

    buf.order(byteOrder);
    return h;
  }

在32位版本的方法调用中，需要传入一个seed。一方面，seed有助于降低冲突碰撞发生的概率。对于不同的数据内容而言，即使散列算法非常优秀，也还是会有产生相同散列值的可能。通过在计算过程中加入seed完成随机数的生成计算，可以进一步降低冲突碰撞的概率。另一方面，对相同的数据内容计算散列值，不同的seed值会产生不同的结果，可以一定程度上避免HashDos安全问题的发生。当然，由于Murmurhash自身是非加密的，所以后一种解释对Murmurhash来说不具有任何意义，Murmurhash更多是期望可以通过seed值来降低冲突碰撞发生的概率。在Murmurhash2中用来生成64位散列值的方法中，seed值被指定为0x1234ABCD。方法调用者只需要关注需要计算散列值的数据内容即可。

在hash()方法的第9行代码中，作者基于传入的seed值生成一个随机数，然后按照每4位得到一个int值来多次进行乘法、位移（右移）和异或操作，直至原始的数据内容全部被处理完或者剩余的数据位数不足4位。在操作过程中使用到的0x5bd1e995和24是事先决定的值，作者之所以取这两个值是因为作者认为这两个值可以产生令人满意的执行结果。作者循环的取出一个int数据（每4位取值），多次执行乘法、位移和异或操作来完成散列值的计算。第23 ~ 30行代码会对剩余的不足4位的数据完成散列值的计算。第32 ~ 34行代码用来保证剩下的最后几位数据在散列之后可以充分的分散在整体的散列结果中。

Murmurhash2 64位实现

public static long hash64A(ByteBuffer buf, int seed) {
    ByteOrder byteOrder = buf.order();
    buf.order(ByteOrder.LITTLE_ENDIAN);

    long m = 0xc6a4a7935bd1e995L;
    int r = 47;

    long h = seed ^ (buf.remaining() * m);

    long k;
    while (buf.remaining() >= 8) {
      k = buf.getLong();

      k *= m;
      k ^= k >>> r;
      k *= m;

      h ^= k;
      h *= m;
    }

    if (buf.remaining() > 0) {
      ByteBuffer finish = ByteBuffer.allocate(8).order(ByteOrder.LITTLE_ENDIAN);
      // for big-endian version, do this first:
      // finish.position(8-buf.remaining());
      finish.put(buf).rewind();
      h ^= finish.getLong();
      h *= m;
    }

    h ^= h >>> r;
    h *= m;
    h ^= h >>> r;

    buf.order(byteOrder);
    return h;
  }

Murmurhash2的缺陷和修复

Murmurhash2的设计中存在一个难以修复的缺陷，我们仍然以32位散列值生成函数来讨论这个缺陷：

如果我们修改程序中的m使之等于1，那么在散列值的计算过程中由于m=1导致k的影响被完全抵消进而产生相同的散列值。即使我们清楚这个问题并严禁将m赋值为1，对同一个输入数据的所有可能散列值也无法达到期望的$ 2^{32} $。

尽管该缺陷难以修复，但在实际的使用场景中，这个缺陷很难让应用程序运行失败。这个缺陷发生的条件非常苛刻：数据内容中包括重复的4字节值，且数据内容的差异仅存在于这些重复的4字节值上，且重复次数位于4字节的边界。如果真的发生了这种情况，那么散列值的范围将由$ 2^{32} $变成$ 2^{27.4} $。

在Murmurhash3中，作者采用了更好的设计来完成散列值的计算，规避了Murmurhash2的设计缺陷，且具有更快的计算速度。

Murmurhash和Java语言的执行测试

下面为一段字符串为例，观察Java提供的String.hashcode()和Murmurhash的执行结果的差异，Murmurhash的实现由Jedis提供。这里对同一个字符串分别用String.hashCode()方法和Murmurhash的算法来生成散列值，需要注意的是，Murmurhash生成的是64位的散列值：

public static void main(String[] args) {
    System.out.println("LiXiansheng01".hashCode());
    System.out.println("LiXiansheng02".hashCode());
    MurmurHash hash = new MurmurHash();
    System.out.println(hash.hash("LiXiansheng01"));
    System.out.println(hash.hash("LiXiansheng02"));
    System.out.println(hash.hash("LiXiansheng03"));
    System.out.println(hash.hash("LiXiansheng04"));
}

代码执行结果如图 - 1所示：

图 - 1

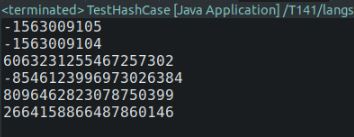
可以看到，Java的String类提供的hashCode()方法虽然简单易行，但是对于字符串差异不大的场景来说，其散列值很容易成为连续的散列值，这样带来的一个不足就是散列值的分布性不够均匀和随机，容易造成聚集。反观Murmurhash的执行结果，即使字符串差异不大，其散列值的差别也是非常大的，这样可以保证散列值具有良好的分布性，尽量减少聚集现象的发生。

基础知识点

雪崩效应（Avalanche effect）

雪崩效应（Avalanche effect）是加密算法的一种理想属性，指的是当输入发生最微小的改变时，会导致输出结果发生比较非常明显的变化。该术语最早由Horst Feistel使用，其概念最早可以追溯到克劳德·香农提出的扩散（diffusion）理论。若某种块密码或加密散列函数没有显示出一定程度的雪崩特性，那么它被认为具有较差的随机化特性，从而密码分析者得以仅仅从输出推测输入。这可能导致该算法部分乃至全部被破解。
严格雪崩准则（Strict Avalanche Criterion，SAC）

严格雪崩准则（Strict Avalanche Criterion，SAC）是雪崩效应的形式化。当任何一个输入位被反转时，输出中的每一位均有50%的概率发生变化。严格雪崩准则建立于密码学的完全性概念上，由Webster和Tavares在1985年提出。
String.hashCode()的思想是什么？

String.hashCode()的实现过程采用了Horner法则（Horner’s rule）的思想，Horner法则也称为秦九韶算法，是一种计算n次多项式的高效算法。Horner法则通过将n次多项式
$f\left( x\right) =a_{n}x^{n}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\ldots \ldots +a_{2}x^{2}+a_{1}x+a_{0}$
转换成
$f\left( x\right) =\left( \left( \left( \ldots \left( \left( a_{n}x+a_{n-1}\right) \cdot x+a_{n-2}\right) \cdot x+a_{n-3}\right) x+\ldots \ldots +a_{2}\right) x+a_{1}\right) x+a_{0}$
这样乘法和加法的计算次数就从n次多项式的$ \dfrac {n\left( n+1\right) }{2} $和 n次，降低到了n次乘法和n次加法，进而提高计算性能。

参考文献

Stack Overflow. What is MurmurHash3 seed parameter? [E]
spacewander. 漫谈非加密哈希算法 [E]
aappleby. SMHasher [E]
Anderson Dadario. Cryptographic and Non-Cryptographic Hash Functions [E]
Wikipedia. MurmurHash [E]