Murmurhash Analysis

Read in Chinese

Murmurhash, invented by Austin Appleby in 2008, is an exceptionally simple, non-cryptographic hash function that can be easily applied in common hash-based lookup scenarios. Murmurhash is notably straightforward, completing all computations in fewer than 52 instructions on X86 architecture machines, resulting in excellent performance. Furthermore, Murmurhash exhibits outstanding avalanche effects and very low collision risks. The term “avalanche effects” refers to the fact that even slight changes in input data produce entirely different hash values, contributing to the excellent distribution of hash values calculated via Murmurhash. The current version of Murmurhash is Murmurhash3, capable of generating a 32-bit or 128-bit hash value. If the result is a 128-bit value, the computation results differ between X86 and X64 architectures. This discussion uses Murmurhash2 as an example.

The author makes certain assumptions and explanations about the operation of Murmurhash in the C code:

Assumes the system can read 4 bytes at once.
Assumes the length of int data is 4 bytes.
Assumes the algorithm does not operate incrementally.
Notes that the algorithm’s results differ between big-endian and little-endian architectures.

This Java code snippet demonstrates the 32-bit version of MurmurHash as implemented in Jedis 3.2.0. It takes a key as input and produces a 32-bit hash value. The code follows the MurmurHash algorithm with the specified assumptions and settings.

public static int hash(ByteBuffer buf, int seed) {
    // save byte order for later restoration
    ByteOrder byteOrder = buf.order();
    buf.order(ByteOrder.LITTLE_ENDIAN);

    int m = 0x5bd1e995;
    int r = 24;

    int h = seed ^ buf.remaining();

    int k;
    while (buf.remaining() >= 4) {
      k = buf.getInt();

      k *= m;
      k ^= k >>> r;
      k *= m;

      h *= m;
      h ^= k;
    }

    if (buf.remaining() > 0) {
      ByteBuffer finish = ByteBuffer.allocate(4).order(ByteOrder.LITTLE_ENDIAN);
      // for big-endian version, use this first:
      // finish.position(4-buf.remaining());
      finish.put(buf).rewind();
      h ^= finish.getInt();
      h *= m;
    }

    h ^= h >>> 13;
    h *= m;
    h ^= h >>> 15;

    buf.order(byteOrder);
    return h;
  }

In the 32-bit version’s method call, you need to provide a seed. On one hand, the seed helps reduce the probability of collisions. Even with an excellent hashing algorithm, there’s still a chance of generating the same hash value for different data. By introducing a seed into the calculation process, random number generation helps further decrease the likelihood of collisions. On the other hand, when calculating hash values for the same data, different seed values yield different results, providing a degree of protection against HashDoS security issues.

However, it’s important to note that since Murmurhash itself is non-cryptographic, the latter explanation regarding HashDoS might not be as relevant. Murmurhash primarily aims to reduce collision probabilities by using seed values. In the method used to generate a 64-bit hash value in Murmurhash2, the seed value is specified as 0x1234ABCD. The method caller only needs to focus on the data content for which the hash value needs to be calculated.

In the hash() method, specifically in the 9th line of code, the author use XORs operation to combine the user-provided seed with the number of remaining bytes in the buffer. This combination helps ensure that different instances of the hash function with different seeds will produce different starting points, even if the remaining bytes are the same. It’s a technique to enhance the randomness and distribution of hash values, especially when dealing with similar or repetitive data. Subsequently, perform multiple multiplication, bitwise shifting (right shift), and XOR operations for every 4 bits, until all original data content has been processed or the remaining data is less than 4 bits. The values 0x5bd1e995 and 24 used in the process are predetermined by the author, chosen because the author believes these values yield satisfactory results.

The author iteratively extracts an int data (taking every 4 bits) within the loop and performs multiple multiplication, bitwise shifting, and XOR operations to calculate the hash value. The code from lines 23 to 30 handles the calculation of the hash value for the remaining data that is less than 4 bits. The code from lines 32 to 34 ensures that the remaining few bits are adequately dispersed in the overall hash result after hashing.

Murmurhash2 64-bit implementation

public static long hash64A(ByteBuffer buf, int seed) {
    ByteOrder byteOrder = buf.order();
    buf.order(ByteOrder.LITTLE_ENDIAN);

    long m = 0xc6a4a7935bd1e995L;
    int r = 47;

    long h = seed ^ (buf.remaining() * m);

    long k;
    while (buf.remaining() >= 8) {
      k = buf.getLong();

      k *= m;
      k ^= k >>> r;
      k *= m;

      h ^= k;
      h *= m;
    }

    if (buf.remaining() > 0) {
      ByteBuffer finish = ByteBuffer.allocate(8).order(ByteOrder.LITTLE_ENDIAN);
      // for big-endian version, do this first:
      // finish.position(8-buf.remaining());
      finish.put(buf).rewind();
      h ^= finish.getLong();
      h *= m;
    }

    h ^= h >>> r;
    h *= m;
    h ^= h >>> r;

    buf.order(byteOrder);
    return h;
  }

The flaw of Murmurhash2

Murmurhash2’s design contains an irremediable flaw, still based on the 32-bit hash function:

If we set the program’s parameter (m) to 1, the calculation of hash values results in complete cancellation of the impact factor (k), and generating identical hash values. Even with awareness and prohibition of setting (m) to 1, achieving the expected $ 2^{32} $ possible hash values for the same input remains unattainable.

While challenging to fix, this flaw is unlikely to cause application failures in practical scenarios. Stringent conditions are required for the flaw to manifest: the data must include repeating 4-byte values, with differences limited to these repetitions and the repetition count aligning with 4-byte boundaries. If such circumstances occur, the hash value range reduces from $ 2^{32} $to $ 2^{27.4} $.

In Murmurhash3, the author employs a superior design for hash value calculation, mitigating the flaw present in Murmurhash2, and offering faster computation.

Tests based on Murmurhash and Java’s hashCode

Below is an example of a string. We’ll observe the differences between the hash codes generated by Java’s String.hashCode() and Murmurhash, implemented by Jedis. It’s important to note that Murmurhash generates a 64-bit hash code for the same string:

public static void main(String[] args) {
    System.out.println("LiXiansheng01".hashCode());
    System.out.println("LiXiansheng02".hashCode());
    MurmurHash hash = new MurmurHash();
    System.out.println(hash.hash("LiXiansheng01"));
    System.out.println(hash.hash("LiXiansheng02"));
    System.out.println(hash.hash("LiXiansheng03"));
    System.out.println(hash.hash("LiXiansheng04"));
}

The execution results of the code are shown in Figure 1：

Figure - 1

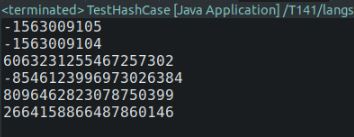
From the results, it’s evident that while Java’s String class provides a straightforward hashCode() method, in scenarios with minimal string differences, its hash codes can easily become consecutive, leading to a lack of uniformity and randomness in hash code distribution, making clustering more likely. On the other hand, observing the results of Murmurhash, even with minor string differences, the hash code differences are significant. This ensures that Murmurhash provides hash codes with a well-distributed pattern, minimizing the occurrence of clustering phenomena.

Supplements

Avalanche effect

The “Avalanche Effect” is an ideal property in encryption algorithms, signifying that even the slightest change in input results in a significantly noticeable change in output. Coined by Horst Feistel, the concept traces back to Claude Shannon’s diffusion theory. In the context of block ciphers or cryptographic hash functions, if a system fails to exhibit a reasonable degree of avalanche effect, it is considered to have poor randomization characteristics. This deficiency could potentially enable cryptanalysts to deduce input solely from the output, posing a risk of partial or complete algorithm compromise.
Strict Avalanche Criterion (SAC)

The “Strict Avalanche Criterion” formalizes the avalanche effect. It dictates that when any input bit is flipped, each output bit should, on average, have a 50% probability of changing. The Strict Avalanche Criterion is grounded in the integrity concepts of cryptography and was introduced by Webster and Tavares in 1985.
The core idea behind String.hashCode()

The implementation process of String.hashCode() utilizes Horner’s rule, also known as Horner’s method or Qin Jiushao’s algorithm. It is an efficient algorithm for computing the value of an nth-degree polynomial. Horner’s rule achieves computational efficiency by transforming an nth-degree polynomial
$f\left( x\right) =a_{n}x^{n}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\ldots \ldots +a_{2}x^{2}+a_{1}x+a_{0}$
into
$f\left( x\right) =\left( \left( \left( \ldots \left( \left( a_{n}x+a_{n-1}\right) \cdot x+a_{n-2}\right) \cdot x+a_{n-3}\right) x+\ldots \ldots +a_{2}\right) x+a_{1}\right) x+a_{0}$
reducing the number of multiplication and addition operations from $ \dfrac {n\left( n+1\right) }{2} $ and n, respectively, to n multiplications and n additions. This optimization enhances computational performance.

References

Stack Overflow. What is MurmurHash3 seed parameter? [E]
spacewander. 漫谈非加密哈希算法 [E]
aappleby. SMHasher [E]
Anderson Dadario. Cryptographic and Non-Cryptographic Hash Functions [E]
Wikipedia. MurmurHash [E]